Ecuación general de la linea recta

Ecuación general de la linea recta

La ecución Ax + By +C = 0 donde A, B, C son números reales y A, B no son simultáneamente nulos, se conoce como la ECUACIÓN GENERAL de primer grado en las variables x e y.

La ecuación explícita de la recta cuando se conocen dos puntos excluye las rectas paralelas al eje y, cuyas ecuaciones son de la forma x = constante, pero todas las rectas del plano, sin excepción, quedan incluidas en la ecuación Ax + By + C = 0 que se conoce como: la ecuación general de la linea recta, como lo afirma el siguiente teorema:

TEOREMA
La ecuación general de primer grado Ax + By + C = 0 (1) , A, B, C

R; A y B no son simultáneamente nulos, representan una linea recta.

Formas de la ecuacion de la recta

Ecuación De La Recta Que Pasa Por El Origen

Tómese sobre la recta los puntos P₁(x₁, y₁),P₂ (x₂, y₂) y P₃(x_3,y₃). Al proyectar los puntos P_1,P₂ y P₃sobre el eje x, se obtienen los puntos P’₁, P’₂, P’₃.
Como los triángulos OP₁P’₁, OP₂P’₂ y OP₃P’₃ son semejantes; se tiene que:

Esto es, cualquiera que sea el punto P(x, y) sobre l,

ó y = mx (1)

La ecuación (1) es la ecuación de la recta que pasa por el origen y tiene pendiente conocida m.

Ecuación De La Recta Conocida Su Pendiente m Y Su Intercepto b Con El Eje y

Trácece por el origen la recta l’ paralela a l. Sea P(x, y) un punto de l. Al llamar P’ la proyección de P sobre el eje x; PP’ corta a la recta l’ en un punto P’’ de coordenadas
P’’(x, Y), Y

y.
Como P’’ (x, Y) está sobre l’, entonces

, de donde Y = mx
Ahora, el cuadrilátero OBPP’’ es un paralelogramo.
Luego, P’’P = OB = b. Y se tiene que:
Y = P’P = P’P’’ + P’’P = Y + b = mx + b.
Es decir, para todo (x, y)

l, y = mx + b = (tan

)x + b
La ecuación y = mx + b es la ecuación de la recta en términos de su pendiente m y su intercepto b con el eje y.

Ecuación De La Recta Que Pasa Por Un Punto Y De Pendiente Conocida

Al restar de la ecuación (2) la ecuación (1) se elimina el parámetro b que se desconoce y se obtiene:

y – y₁ = m(x – x₁) (3)

La ecuación (3) es conocida como la forma: PUNTO-PENDIENTE de la ecuación de la recta.
Nótese que la ecuación (3) también puede escribirse en la forma:
y = mx + (y₁ – mx₁).
Lo que indica que el intercepto b con el eje y viene dado por:
b = y₁ – mx₁

Ecuación de la recta que pasa por dos puntos dados P₁(x₁, y₁) y P₂(x₂, y₂)

Como l pasa por el punto P₁(x₁, y₁) y tiene pendiente m₁, se tiene de acuerdo a 4.4.3, que
y – y₁ = m₁ (x – x1) (1)
representa la ecuación de dicha recta.
Ahora, como el punto P₂(x₂, y₂)

l, entonces satisface su ecuación.
Esto es y₂ – y₁ =

; de donde

(2)
Sustituyendo (2) en (1) se obtiene

(3)

La ecuación (3) se conoce como la forma: DOS-PUNTOS de la ecuación de la recta.

Propiedades de la recta

PROPIEDADES DE LA RECTA:

I. Dos rectas se intersecan en un punto, y sólo en uno.

II. Si fuera de una recta se encuentra un punto, el punto y la recta están contenidos en un plano, y sólo en uno.

III. Si dos rectas se intersecan, ambas están contenidos en un plano, y sólo en uno.

IV. Si en una misma recta están tres puntos, no más de uno está situado entre los otros dos.

V. En un rayo existe un punto, y sólo uno, situado a una distancia dada del punto extremo del rayo.

VI. Un segmento tiene un punto medio y sólo uno.

La ecuación general de la recta es de la siguiente forma:

ax+by+c=0

Coordenadas Polares

Coordenadas polares

El sistema de coordenadas polares es un sistema de coordenadas bidimensional en el cual cada punto o posición del plano se determina por un ángulo y una distancia.

De manera más precisa, todo punto del plano corresponde a un par de coordenadas (r, θ) donde r es la distancia del punto al origen o polo y θ es el ángulo positivo en sentido antihorario medido desde el eje polar (equivalente al eje x del sistema cartesiano). La distancia se conoce como la «coordenada radial» mientras que el ángulo es la «coordenada angular» o «ángulo polar».
En el caso del origen de coordenadas, el valor de r es cero, pero el valor de θ es indefinido. En ocasiones se adopta la convención de representar el origen por (0,0º).

Conversión de coordenadas polares a rectangulares

Definido un punto en coordenadas polares por su ángulo

θ

sobre el eje x, y su distancia r al centro de coordenadas, se tiene:

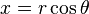
$x= r \cos \theta \,$

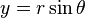
$y= r \sin \theta \,$

Conversión de coordenadas rectangulares a polares

Definido un punto del plano por sus coordenadas rectangulares (x,y), se tiene que la coordenada polar r es:

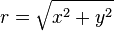$r= \sqrt{x^2 +y^2}$ (aplicando el Teorema de Pitágoras)

Para determinar la coordenada angular θ, se deben distinguir dos casos:

Para $r$ = 0, el ángulo θ puede tomar cualquier valor real.
Para $r$ ≠ 0, para obtener un único valor de θ, debe limitarse a un intervalo de tamaño 2π. Por convención, los intervalos utilizados son [0, 2π) y (−π, π].

Para obtener θ en el intervalo [0, 2π), se deben usar las siguientes fórmulas (

arctan

denota la inversa de la función tangente):

$\theta = \begin{cases} \arctan(\frac{y}{x}) & \mbox{si } x > 0 \mbox{ y } y \ge 0\\ \arctan(\frac{y}{x}) + 2\pi & \mbox{si } x > 0 \mbox{ y } y < 0\\ \arctan(\frac{y}{x}) + \pi & \mbox{si } x < 0\\ \frac{\pi}{2} & \mbox{si } x = 0 \mbox{ y } y > 0\\ \frac{3\pi}{2} & \mbox{si } x = 0 \mbox{ y } y < 0 \end{cases}$

Para obtener θ en el intervalo (−π, π], se deben usar las siguientes fórmulas:

$\theta = \begin{cases} \arctan(\frac{y}{x}) & \mbox{si } x > 0\\ \arctan(\frac{y}{x}) + \pi & \mbox{si } x < 0 \mbox{ y } y \ge 0\\ \arctan(\frac{y}{x}) - \pi & \mbox{si } x < 0 \mbox{ y } y < 0\\ \frac{\pi}{2} & \mbox{si } x = 0 \mbox{ y } y > 0\\ -\frac{\pi}{2} & \mbox{si } x = 0 \mbox{ y } y < 0 \end{cases}$

Muchos lenguajes de programación modernos evitan tener que almacenar el signo del numerador y del denominador gracias a la implementación de la función atan2, que tiene argumentos separados para el numerador y el denominador. En los lenguajes que permiten argumentos opcionales, la función atan puede recibir como parámetro la coordenada x (como ocurre en Lisp).

Division de un Segmento en una Razon Dada

DIVISIÓN DE UN SEGMENTO EN UNA RAZÓN DADA

El resultado de la comparación de dos cantidades de la misma especie, se llama razón o relación de dichas cantidades. Las razones o relaciones pueden ser razones por cociente o geométricas.

La razón por cociente o geométrica es el resultado de la comparación de dos cantidades homogéneas con el objeto de saber cuantas veces la una contiene a la otra.

Observación: En geometría analítica las razones deben considerarse con su signo o sentido porque se trata de segmentos de recta dirigidos.

Consideramos los puntos A(X1,Y1) y B(X2, Y2) los extremos de una recta. Sea P(X, Y) el punto de división que se encuentra entre la recta.

Punto Medio

Punto Medio

Punto medio o punto equidistante, en matemática, es el punto que se encuentra a la misma distancia de cualquiera de los extremos.

Si es un segmento acotado, el punto medio es el que lo divide en dos partes iguales. En ese caso, el punto medio es único y equidista de los extremos del segmento. Por cumplir esta última condición, pertenece a la mediatriz del segmento.

Las formulas son:

X=(X1+X2) Y=(Y1+Y)

2 2

Puntos en un Plano Carteciano

Puntos en un Plano Carteciano

la distancia entre dos puntos se puede precentar en dos formas las cuales explicaremos a continuacion:

Caso1:

Sean los puntos P1=(x,y) y P2(x,y) dos puntos localizados de forma general en un plano y que pertenecen a una misma recta horizontal, (paralela al eje x) la distancia dirijida entre los dos puntos es:

Formulas de distancia dirijidas:

P1 al P2 o P2 al P1

Formula de la distancia no dirijida o absoluta:

P1 al P2= X1-X2

P2 al P1= X2-X1

Caso 2:

Sean el punto 1(X1Y1) y punto 2(X2Y2) dos puntos pertenecientes a una misma recta vertical (Paralela al eje Y), la distancia dirijida entre los dos puntos es:

Formulas de distancia dirijidas:

P1 al P2 o P2 al P1

P1 al P2= Y1-Y2

P2 al P1= Y2-Y1

Plano carteciano

Plano Carteciano

El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen.

El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados. Las coordenadas se forman asociando un valordel eje de las "X" y uno de las "Y", respectivamente, esto indica que un punto se puede ubicar en el plano cartesiano con base en sus coordenadas.

Geometria Analitica

Geometria Analitica

Geometría Analítica: Es estudio de ciertos objetos geométricos mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas.

Los dos problemas fundamentales de la geometría analítica son:

Dado el lugar geométrico en un sistema de coordenadas, obtener su ecuación.
Dada la ecuación en un sistema de coordenadas, determinar la gráfica o lugar geométrico de los puntos que verifican # dicha ecuación.

miércoles, 8 de diciembre de 2010

Coordenadas polares

Conversión de coordenadas polares a rectangulares

Conversión de coordenadas rectangulares a polares